Let 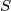 be a finite set of points in three-dimensional space. Let
be a finite set of points in three-dimensional space. Let 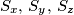 be the sets consisting of the orthogonal projections of the points of
be the sets consisting of the orthogonal projections of the points of 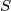 onto the
onto the 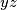 -plane,
-plane,  -plane,
-plane, 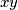 -plane, respectively. Prove that
-plane, respectively. Prove that 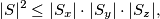 where
where 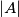 denotes the number of elements in the finite set
denotes the number of elements in the finite set  .
.
Note Note: The orthogonal projection of a point onto a plane is the foot of the perpendicular from that point to the plane.
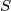 be a finite set of points in three-dimensional space. Let
be a finite set of points in three-dimensional space. Let 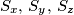 be the sets consisting of the orthogonal projections of the points of
be the sets consisting of the orthogonal projections of the points of 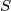 onto the
onto the 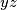 -plane,
-plane,  -plane,
-plane, 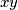 -plane, respectively. Prove that
-plane, respectively. Prove that 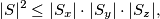 where
where 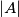 denotes the number of elements in the finite set
denotes the number of elements in the finite set  .
. Note Note: The orthogonal projection of a point onto a plane is the foot of the perpendicular from that point to the plane.
 Školjka
Školjka