Središte

upisane kružnice trokuta

spojeno je dužinama s njegovim vrhovima. Neka su
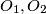
i
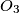
središta kružnica opisanih trokutima
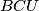
,
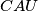
i
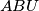
. Dokažite da kružnice opisane trokutima

i

imaju zajedničko središte.
%V0
Središte $U$ upisane kružnice trokuta $ABC$ spojeno je dužinama s njegovim vrhovima. Neka su $O_1, O_2$ i $O_3$ središta kružnica opisanih trokutima $BCU$, $CAU$ i $ABU$. Dokažite da kružnice opisane trokutima $ABC$ i $O_1O_2O_3$ imaju zajedničko središte.