Let
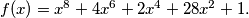
Let
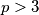
be a prime and suppose there exists an integer
such that
divides
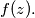
Prove that there exist integers
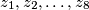
such that if
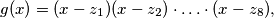
then all coefficients of
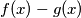
are divisible by
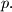
%V0
Let $f(x) = x^8 + 4x^6 + 2x^4 + 28x^2 + 1.$ Let $p > 3$ be a prime and suppose there exists an integer $z$ such that $p$ divides $f(z).$ Prove that there exist integers $z_1, z_2, \ldots, z_8$ such that if $$g(x) = (x - z_1)(x - z_2) \cdot \ldots \cdot (x - z_8),$$ then all coefficients of $f(x) - g(x)$ are divisible by $p.$
Školjka