Show that there exists a finite set
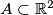
such that for every
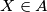
there are points
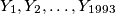
in
such that the distance between
and
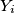
is equal to 1, for every
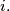
%V0
Show that there exists a finite set $A \subset \mathbb{R}^2$ such that for every $X \in A$ there are points $Y_1, Y_2, \ldots, Y_{1993}$ in $A$ such that the distance between $X$ and $Y_i$ is equal to 1, for every $i.$
Školjka