Let
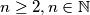
and
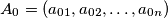
be any
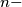
tuple of natural numbers, such that
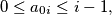
for
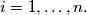
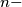
tuples
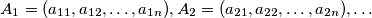
are defined by:
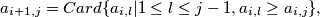
for
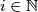
and
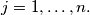
Prove that there exists
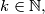
such that
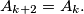
%V0
Let $n \geq 2, n \in \mathbb{N}$ and $A_0 = (a_{01},a_{02}, \ldots, a_{0n})$ be any $n-$tuple of natural numbers, such that $0 \leq a_{0i} \leq i-1,$ for $i = 1, \ldots, n.$
$n-$tuples $A_1= (a_{11},a_{12}, \ldots, a_{1n}), A_2 = (a_{21},a_{22}, \ldots, a_{2n}), \ldots$ are defined by: $a_{i+1,j} = Card \{a_{i,l}| 1 \leq l \leq j-1, a_{i,l} \geq a_{i,j}\},$ for $i \in \mathbb{N}$ and $j = 1, \ldots, n.$ Prove that there exists $k \in \mathbb{N},$ such that $A_{k+2} = A_{k}.$