A circle  bisects a circle
bisects a circle 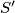 if it cuts
if it cuts 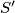 at opposite ends of a diameter.
at opposite ends of a diameter. 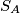 ,
, 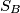 ,
,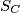 are circles with distinct centers
are circles with distinct centers 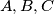 (respectively).
(respectively).
Show that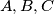 are collinear iff there is no unique circle
are collinear iff there is no unique circle  which bisects each of
which bisects each of 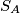 ,
, 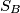 ,
,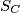 . Show that if there is more than one circle
. Show that if there is more than one circle  which bisects each of
which bisects each of 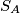 ,
, 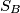 ,
,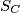 , then all such circles pass through two fixed points. Find these points.
, then all such circles pass through two fixed points. Find these points.
Original Statement:
A circle is said to cut a circle
is said to cut a circle 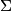 diametrically if and only if their common chord is a diameter of
diametrically if and only if their common chord is a diameter of 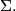
Let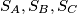 be three circles with distinct centres
be three circles with distinct centres 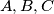 respectively. Prove that
respectively. Prove that 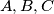 are collinear if and only if there is no unique circle
are collinear if and only if there is no unique circle  which cuts each of
which cuts each of 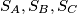 diametrically. Prove further that if there exists more than one circle
diametrically. Prove further that if there exists more than one circle  which cuts each
which cuts each 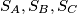 diametrically, then all such circles
diametrically, then all such circles  pass through two fixed points. Locate these points in relation to the circles
pass through two fixed points. Locate these points in relation to the circles 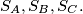
 bisects a circle
bisects a circle 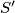 if it cuts
if it cuts 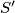 at opposite ends of a diameter.
at opposite ends of a diameter. 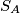 ,
, 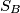 ,
,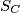 are circles with distinct centers
are circles with distinct centers 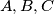 (respectively).
(respectively). Show that
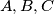 are collinear iff there is no unique circle
are collinear iff there is no unique circle  which bisects each of
which bisects each of 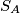 ,
, 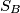 ,
,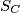 . Show that if there is more than one circle
. Show that if there is more than one circle  which bisects each of
which bisects each of 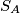 ,
, 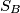 ,
,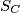 , then all such circles pass through two fixed points. Find these points.
, then all such circles pass through two fixed points. Find these points. Original Statement:
A circle
 is said to cut a circle
is said to cut a circle 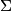 diametrically if and only if their common chord is a diameter of
diametrically if and only if their common chord is a diameter of 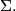
Let
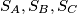 be three circles with distinct centres
be three circles with distinct centres 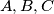 respectively. Prove that
respectively. Prove that 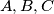 are collinear if and only if there is no unique circle
are collinear if and only if there is no unique circle  which cuts each of
which cuts each of 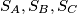 diametrically. Prove further that if there exists more than one circle
diametrically. Prove further that if there exists more than one circle  which cuts each
which cuts each 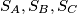 diametrically, then all such circles
diametrically, then all such circles  pass through two fixed points. Locate these points in relation to the circles
pass through two fixed points. Locate these points in relation to the circles 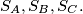
 Školjka
Školjka