On an infinite chessboard, a solitaire game is played as follows: at the start, we have 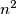 pieces occupying a square of side
pieces occupying a square of side  The only allowed move is to jump over an occupied square to an unoccupied one, and the piece which has been jumped over is removed. For which
The only allowed move is to jump over an occupied square to an unoccupied one, and the piece which has been jumped over is removed. For which  can the game end with only one piece remaining on the board?
can the game end with only one piece remaining on the board?
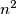 pieces occupying a square of side
pieces occupying a square of side  The only allowed move is to jump over an occupied square to an unoccupied one, and the piece which has been jumped over is removed. For which
The only allowed move is to jump over an occupied square to an unoccupied one, and the piece which has been jumped over is removed. For which  can the game end with only one piece remaining on the board?
can the game end with only one piece remaining on the board?  Školjka
Školjka