For three points
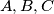
in the plane, we define
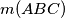
to be the smallest length of the three heights of the triangle

, where in the case

,

,

are collinear, we set
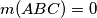
. Let

,

,

be given points in the plane. Prove that for any point

in the plane,
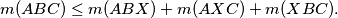
%V0
For three points $A,B,C$ in the plane, we define $m(ABC)$ to be the smallest length of the three heights of the triangle $ABC$, where in the case $A$, $B$, $C$ are collinear, we set $m(ABC) = 0$. Let $A$, $B$, $C$ be given points in the plane. Prove that for any point $X$ in the plane,
$$m(ABC) \leq m(ABX) + m(AXC) + m(XBC).$$