Let
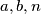
be positive integers,
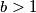
and
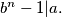
Show that the representation of the number

in the base

contains at least

digits different from zero.
%V0
Let $a,b,n$ be positive integers, $b > 1$ and $b^n-1|a.$ Show that the representation of the number $a$ in the base $b$ contains at least $n$ digits different from zero.