Let
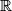
denote the set of all real numbers and
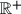
the subset of all positive ones. Let

and

be given elements in
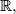
not necessarily distinct. Find all functions
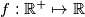
such that
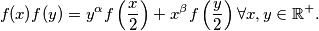
%V0
Let $\mathbb{R}$ denote the set of all real numbers and $\mathbb{R}^+$ the subset of all positive ones. Let $\alpha$ and $\beta$ be given elements in $\mathbb{R},$ not necessarily distinct. Find all functions $f: \mathbb{R}^+ \mapsto \mathbb{R}$ such that
$$f(x)f(y) = y^{\alpha} f \left( \frac{x}{2} \right) + x^{\beta} f \left( \frac{y}{2} \right) \forall x,y \in \mathbb{R}^+.$$