A circle  with center
with center 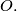 and a line
and a line  which does not touch circle
which does not touch circle 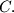
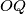 is perpendicular to
is perpendicular to 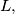
 is on
is on 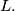
 is on
is on 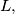 draw two tangents
draw two tangents 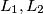 to circle
to circle 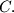
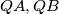 are perpendicular to
are perpendicular to 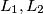 respectively. (
respectively. ( on
on 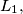
 on
on 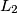 ). Prove that, line
). Prove that, line  intersect
intersect 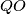 at a fixed point.
at a fixed point.
Original formulation:
A line does not meet a circle
does not meet a circle  with center
with center 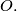
 is the point on
is the point on  such that
such that 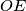 is perpendicular to
is perpendicular to 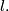
 is any point on
is any point on  other than
other than 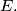 The tangents from
The tangents from  to
to  touch it at
touch it at  and
and 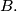
 is the point on
is the point on 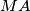 such that
such that 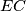 is perpendicular to
is perpendicular to 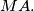
 is the point on
is the point on 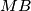 such that
such that 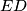 is perpendicular to
is perpendicular to 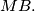 The line
The line  cuts
cuts 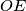 at
at 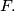 Prove that the location of
Prove that the location of  is independent of that of
is independent of that of 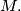
 with center
with center 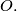 and a line
and a line  which does not touch circle
which does not touch circle 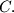
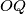 is perpendicular to
is perpendicular to 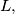
 is on
is on 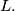
 is on
is on 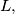 draw two tangents
draw two tangents 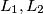 to circle
to circle 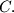
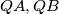 are perpendicular to
are perpendicular to 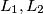 respectively. (
respectively. ( on
on 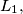
 on
on 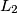 ). Prove that, line
). Prove that, line  intersect
intersect 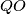 at a fixed point.
at a fixed point. Original formulation:
A line
 does not meet a circle
does not meet a circle  with center
with center 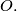
 is the point on
is the point on  such that
such that 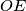 is perpendicular to
is perpendicular to 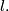
 is any point on
is any point on  other than
other than 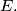 The tangents from
The tangents from  to
to  touch it at
touch it at  and
and 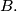
 is the point on
is the point on 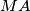 such that
such that 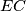 is perpendicular to
is perpendicular to 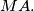
 is the point on
is the point on 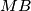 such that
such that 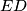 is perpendicular to
is perpendicular to 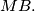 The line
The line  cuts
cuts 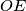 at
at 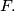 Prove that the location of
Prove that the location of  is independent of that of
is independent of that of 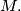
 Školjka
Školjka