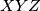A circle  with center
with center 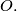 and a line
and a line  which does not touch circle
which does not touch circle 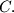
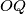 is perpendicular to
is perpendicular to 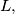
 is on
is on 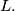
 is on
is on 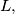 draw two tangents
draw two tangents 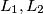 to circle
to circle 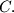
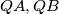 are perpendicular to
are perpendicular to 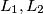 respectively. (
respectively. ( on
on 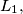
 on
on 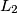 ). Prove that, line
). Prove that, line  intersect
intersect 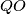 at a fixed point.
at a fixed point.
Original formulation:
A line does not meet a circle
does not meet a circle  with center
with center 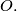
 is the point on
is the point on  such that
such that 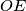 is perpendicular to
is perpendicular to 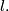
 is any point on
is any point on  other than
other than 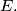 The tangents from
The tangents from  to
to  touch it at
touch it at  and
and 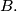
 is the point on
is the point on 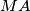 such that
such that 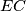 is perpendicular to
is perpendicular to 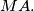
 is the point on
is the point on 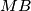 such that
such that 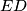 is perpendicular to
is perpendicular to 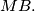 The line
The line  cuts
cuts 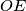 at
at 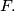 Prove that the location of
Prove that the location of  is independent of that of
is independent of that of 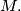
 with center
with center 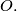 and a line
and a line  which does not touch circle
which does not touch circle 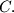
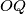 is perpendicular to
is perpendicular to 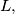
 is on
is on 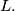
 is on
is on 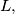 draw two tangents
draw two tangents 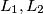 to circle
to circle 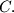
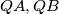 are perpendicular to
are perpendicular to 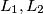 respectively. (
respectively. ( on
on 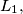
 on
on 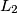 ). Prove that, line
). Prove that, line  intersect
intersect 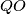 at a fixed point.
at a fixed point. Original formulation:
A line
 does not meet a circle
does not meet a circle  with center
with center 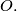
 is the point on
is the point on  such that
such that 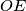 is perpendicular to
is perpendicular to 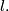
 is any point on
is any point on  other than
other than 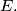 The tangents from
The tangents from  to
to  touch it at
touch it at  and
and 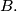
 is the point on
is the point on 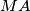 such that
such that 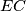 is perpendicular to
is perpendicular to 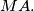
 is the point on
is the point on 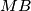 such that
such that 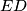 is perpendicular to
is perpendicular to 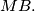 The line
The line  cuts
cuts 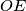 at
at 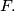 Prove that the location of
Prove that the location of  is independent of that of
is independent of that of 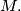
 Školjka
Školjka  . Prove that there exists a point
. Prove that there exists a point 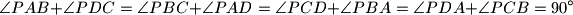
 and
and  are perpendicular.
are perpendicular. 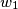 and
and 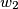 with centres
with centres 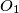 and
and 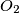 are externally tangent at point
are externally tangent at point  at points
at points  is the common tangent of
is the common tangent of 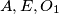 are on the same side of
are on the same side of 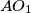 ,
, 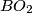 ,
,  and
and 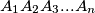 be a regular n-gon. Let
be a regular n-gon. Let  and
and 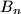 be the midpoints of its sides
be the midpoints of its sides 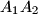 and
and 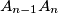 . Also, for every
. Also, for every 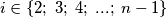 , let
, let  be the point of intersection of the lines
be the point of intersection of the lines 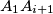 and
and 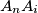 , and let
, and let 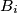 be the point of intersection of the angle bisector bisector of the angle
be the point of intersection of the angle bisector bisector of the angle 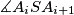 with the segment
with the segment 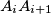 .
. 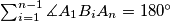 .
.  . Denote by
. Denote by  a point inside the quadrilateral
a point inside the quadrilateral 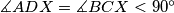 and
and 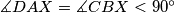 . Show that
. Show that 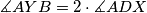 .
. 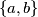 and
and 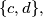 respectively, with
respectively, with 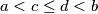 and
and 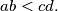 Prove that the first rectangle can be placed within the second one if and only if
Prove that the first rectangle can be placed within the second one if and only if 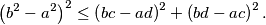
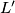 and
and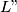 . A circle
. A circle 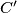 touches
touches 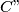 touches
touches  . The lines
. The lines 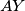 and
and 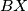 meet at
meet at