Show that there exists a set

of positive integers with the following property: for any infinite set

of primes, there exist two positive integers

in

and

not in

, each of which is a product of

distinct elements of

for some
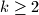
.
%V0
Show that there exists a set $A$ of positive integers with the following property: for any infinite set $S$ of primes, there exist two positive integers $m$ in $A$ and $n$ not in $A$, each of which is a product of $k$ distinct elements of $S$ for some $k \geq 2$.