Define the sequences
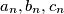
as follows.
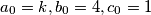
.
If

is even then
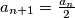
,
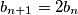
,
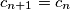
.
If

is odd, then
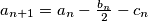
,
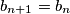
,
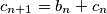
.
Find the number of positive integers
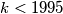
such that some
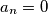
.
%V0
Define the sequences $a_n, b_n, c_n$ as follows. $a_0 = k, b_0 = 4, c_0 = 1$.
If $a_n$ is even then $a_{n + 1} = \frac {a_n}{2}$, $b_{n + 1} = 2b_n$, $c_{n + 1} = c_n$.
If $a_n$ is odd, then $a_{n + 1} = a_n - \frac {b_n}{2} - c_n$, $b_{n + 1} = b_n$, $c_{n + 1} = b_n + c_n$.
Find the number of positive integers $k < 1995$ such that some $a_n = 0$.