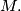Slični zadaci
We define a sequence 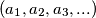 by setting
by setting
![a_{n} = \frac {1}{n}\left(\left[\frac {n}{1}\right] + \left[\frac {n}{2}\right] + \cdots + \left[\frac {n}{n}\right]\right)](/media/m/0/f/c/0fcd7236589e4454f518b8d8aa9fe147.png)
for every positive integer . Hereby, for every real
. Hereby, for every real  , we denote by
, we denote by ![\left[x\right]](/media/m/3/6/9/3697c66f8530757a1166f24a1fd325e6.png) the integral part of
the integral part of  (this is the greatest integer which is
(this is the greatest integer which is 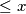 ).
).
a) Prove that there is an infinite number of positive integers such that
such that 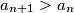 .
.
b) Prove that there is an infinite number of positive integers such that
such that 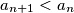 .
.
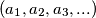 by setting
by setting ![a_{n} = \frac {1}{n}\left(\left[\frac {n}{1}\right] + \left[\frac {n}{2}\right] + \cdots + \left[\frac {n}{n}\right]\right)](/media/m/0/f/c/0fcd7236589e4454f518b8d8aa9fe147.png)
for every positive integer
 . Hereby, for every real
. Hereby, for every real  , we denote by
, we denote by ![\left[x\right]](/media/m/3/6/9/3697c66f8530757a1166f24a1fd325e6.png) the integral part of
the integral part of  (this is the greatest integer which is
(this is the greatest integer which is 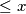 ).
). a) Prove that there is an infinite number of positive integers
 such that
such that 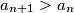 .
. b) Prove that there is an infinite number of positive integers
 such that
such that 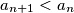 .
.  Školjka
Školjka 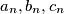 as follows.
as follows. 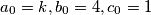 .
. 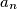 is even then
is even then 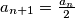 ,
, 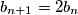 ,
, 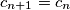 .
. 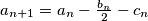 ,
, 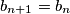 ,
, 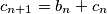 .
. 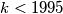 such that some
such that some 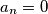 .
. 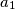 ,
, 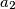 , ...,
, ..., 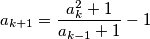 for every
for every  with
with 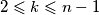 .
.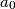 ,
,  be a sequence of positive integers such that the greatest common divisor of any two consecutive terms is greater than the preceding term; in symbols,
be a sequence of positive integers such that the greatest common divisor of any two consecutive terms is greater than the preceding term; in symbols, 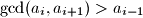 . Prove that
. Prove that 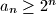 for all
for all 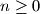 .
. 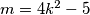 . Show that there exist positive integers
. Show that there exist positive integers  and
and  such that the sequence
such that the sequence 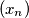 defined by
defined by 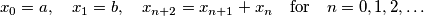 has all of its terms relatively prime to
has all of its terms relatively prime to  .
. 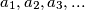 as follows.
as follows. 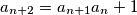 . Show that for every
. Show that for every 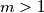 there is an
there is an 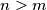 such that
such that 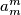 divides
divides 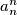 . Is it true that
. Is it true that 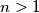 ?
?  is a subset of
is a subset of 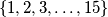 such that the product of any three distinct elements of
such that the product of any three distinct elements of