Define the sequence
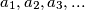
as follows.
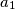
and
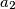
are coprime positive integers and
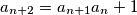
. Show that for every
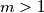
there is an
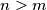
such that
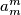
divides
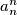
. Is it true that
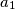
must divide
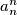
for some
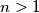
?
%V0
Define the sequence $a_1, a_2, a_3, ...$ as follows. $a_1$ and $a_2$ are coprime positive integers and $a_{n + 2} = a_{n + 1}a_n + 1$. Show that for every $m > 1$ there is an $n > m$ such that $a_m^m$ divides $a_n^n$. Is it true that $a_1$ must divide $a_n^n$ for some $n > 1$?