Slični zadaci
We define a sequence 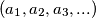 by setting
by setting
![a_{n} = \frac {1}{n}\left(\left[\frac {n}{1}\right] + \left[\frac {n}{2}\right] + \cdots + \left[\frac {n}{n}\right]\right)](/media/m/0/f/c/0fcd7236589e4454f518b8d8aa9fe147.png)
for every positive integer . Hereby, for every real
. Hereby, for every real  , we denote by
, we denote by ![\left[x\right]](/media/m/3/6/9/3697c66f8530757a1166f24a1fd325e6.png) the integral part of
the integral part of  (this is the greatest integer which is
(this is the greatest integer which is 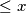 ).
).
a) Prove that there is an infinite number of positive integers such that
such that 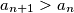 .
.
b) Prove that there is an infinite number of positive integers such that
such that 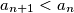 .
.
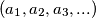 by setting
by setting ![a_{n} = \frac {1}{n}\left(\left[\frac {n}{1}\right] + \left[\frac {n}{2}\right] + \cdots + \left[\frac {n}{n}\right]\right)](/media/m/0/f/c/0fcd7236589e4454f518b8d8aa9fe147.png)
for every positive integer
 . Hereby, for every real
. Hereby, for every real  , we denote by
, we denote by ![\left[x\right]](/media/m/3/6/9/3697c66f8530757a1166f24a1fd325e6.png) the integral part of
the integral part of  (this is the greatest integer which is
(this is the greatest integer which is 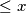 ).
). a) Prove that there is an infinite number of positive integers
 such that
such that 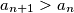 .
. b) Prove that there is an infinite number of positive integers
 such that
such that 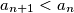 .
.  Školjka
Školjka 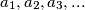 as follows.
as follows.  and
and 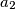 are coprime positive integers and
are coprime positive integers and 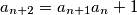 . Show that for every
. Show that for every 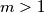 there is an
there is an 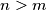 such that
such that 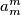 divides
divides 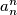 . Is it true that
. Is it true that 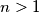 ?
?  be a positive integer. Show that if there exists a sequence
be a positive integer. Show that if there exists a sequence 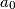 ,
, 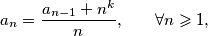 then
then 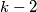 is divisible by
is divisible by  .
. satisfying
satisfying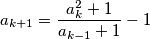 for every
for every 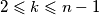 .
. be a sequence of positive integers such that the greatest common divisor of any two consecutive terms is greater than the preceding term; in symbols,
be a sequence of positive integers such that the greatest common divisor of any two consecutive terms is greater than the preceding term; in symbols, 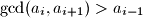 . Prove that
. Prove that 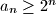 for all
for all 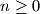 .
. 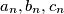 as follows.
as follows. 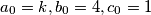 .
. 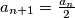 ,
, 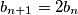 ,
, 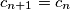 .
. 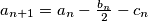 ,
, 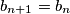 ,
, 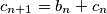 .
. 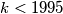 such that some
such that some 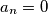 .
.