Let

be an integer,
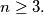
Let
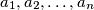
be real numbers such that
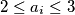
for
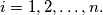
If
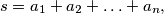
prove that
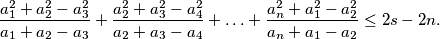
%V0
Let $n$ be an integer, $n \geq 3.$ Let $a_1, a_2, \ldots, a_n$ be real numbers such that $2 \leq a_i \leq 3$ for $i = 1, 2, \ldots, n.$ If $s = a_1 + a_2 + \ldots + a_n,$ prove that $$\frac{a^{2}_{1}+a^{2}_{2}-a^{2}_{3}}{a_{1}+a_{2}-a_{3}}+\frac{a^{2}_{2}+a^{2}_{3}-a^{2}_{4}}{a_{2}+a_{3}-a_{4}}+\ldots+\frac{a^{2}_{n}+a^{2}_{1}-a^{2}_{2}}{a_{n}+a_{1}-a_{2}}\leq 2s-2n.$$