Let
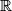
be the set of real numbers. Does there exist a function
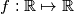
which simultaneously satisfies the following three conditions?
(a) There is a positive number

such that
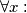
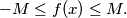
(b) The value of
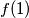
is
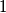
.
(c) If
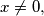
then
![f \left(x + \frac {1}{x^2} \right) = f(x) + \left[ f \left(\frac {1}{x} \right) \right]^2](/media/m/0/c/f/0cf2538c4d8a135349370aeaece3cd1b.png)
%V0
Let $\mathbb{R}$ be the set of real numbers. Does there exist a function $f: \mathbb{R} \mapsto \mathbb{R}$ which simultaneously satisfies the following three conditions?
(a) There is a positive number $M$ such that $\forall x:$ $- M \leq f(x) \leq M.$
(b) The value of $f(1)$ is $1$.
(c) If $x \neq 0,$ then
$$f \left(x + \frac {1}{x^2} \right) = f(x) + \left[ f \left(\frac {1}{x} \right) \right]^2$$