Let

be an integer,
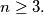
Let
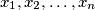
be real numbers such that
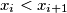
for
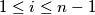
. Prove that
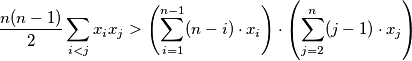
%V0
Let $n$ be an integer,$n \geq 3.$ Let $x_1, x_2, \ldots, x_n$ be real numbers such that $x_i < x_{i+1}$ for $1 \leq i \leq n - 1$. Prove that
$$\frac{n(n-1)}{2}\sum_{i < j}x_{i}x_{j}>\left(\sum^{n-1}_{i=1}(n-i)\cdot x_{i}\right)\cdot\left(\sum^{n}_{j=2}(j-1)\cdot x_{j}\right)$$