Let
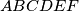
be a convex hexagon with
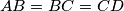
and
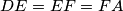
, such that
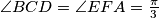
. Suppose
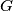
and
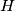
are points in the interior of the hexagon such that
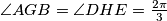
. Prove that
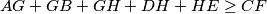
.
%V0
Let $ABCDEF$ be a convex hexagon with $AB = BC = CD$ and $DE = EF = FA$, such that $\angle BCD = \angle EFA = \frac {\pi}{3}$. Suppose $G$ and $H$ are points in the interior of the hexagon such that $\angle AGB = \angle DHE = \frac {2\pi}{3}$. Prove that $AG + GB + GH + DH + HE \geq CF$.