Determine all integers
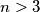
for which there exist

points
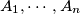
in the plane, no three collinear, and real numbers
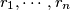
such that for
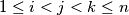
, the area of
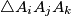
is
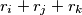
.
%V0
Determine all integers $n > 3$ for which there exist $n$ points $A_{1},\cdots ,A_{n}$ in the plane, no three collinear, and real numbers $r_{1},\cdots ,r_{n}$ such that for $1\leq i < j < k\leq n$, the area of $\triangle A_{i}A_{j}A_{k}$ is $r_{i} + r_{j} + r_{k}$.