Let

be an odd prime number. How many

-element subsets

of
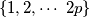
are there, the sum of whose elements is divisible by

?
%V0
Let $p$ be an odd prime number. How many $p$-element subsets $A$ of $\{1,2,\cdots \ 2p\}$ are there, the sum of whose elements is divisible by $p$?