Let
be an odd prime. Determine positive integers
and
for which
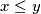
and
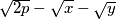
is non-negative and as small as possible.
%V0
Let $p$ be an odd prime. Determine positive integers $x$ and $y$ for which $x \leq y$ and $\sqrt{2p} - \sqrt{x} - \sqrt{y}$ is non-negative and as small as possible.
Školjka