Let  be an even positive integer. Prove that there exists a positive integer
be an even positive integer. Prove that there exists a positive integer  such that
such that
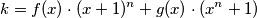
for some polynomials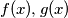 having integer coefficients. If
having integer coefficients. If 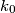 denotes the least such
denotes the least such 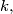 determine
determine 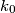 as a function of
as a function of 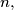 i.e. show that
i.e. show that 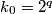 where
where 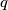 is the odd integer determined by
is the odd integer determined by 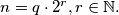
Note: This is variant A6' of the three variants given for this problem.
 be an even positive integer. Prove that there exists a positive integer
be an even positive integer. Prove that there exists a positive integer  such that
such that 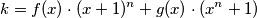
for some polynomials
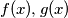 having integer coefficients. If
having integer coefficients. If 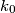 denotes the least such
denotes the least such 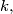 determine
determine 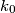 as a function of
as a function of 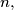 i.e. show that
i.e. show that 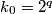 where
where 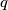 is the odd integer determined by
is the odd integer determined by 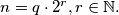
Note: This is variant A6' of the three variants given for this problem.
 Školjka
Školjka