Let

be a function from the set of real numbers
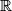
into itself such for all
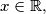
we have

and
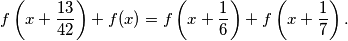
Prove that

is a periodic function (that is, there exists a non-zero real number

such
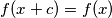
for all
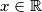
).
%V0
Let $f$ be a function from the set of real numbers $\mathbb{R}$ into itself such for all $x \in \mathbb{R},$ we have $|f(x)| \leq 1$ and
$$f \left( x + \frac{13}{42} \right) + f(x) = f \left( x + \frac{1}{6} \right) + f \left( x + \frac{1}{7} \right).$$
Prove that $f$ is a periodic function (that is, there exists a non-zero real number $c$ such $f(x+c) = f(x)$ for all $x \in \mathbb{R}$).