Let
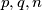
be three positive integers with
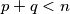
. Let
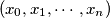
be an
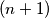
-tuple of integers satisfying the following conditions :
(a)
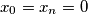
, and
(b) For each

with
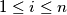
, either
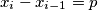
or
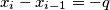
.
Show that there exist indices
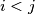
with
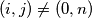
, such that
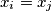
.
%V0
Let $p,q,n$ be three positive integers with $p + q < n$. Let $(x_{0},x_{1},\cdots ,x_{n})$ be an $(n + 1)$-tuple of integers satisfying the following conditions :
(a) $x_{0} = x_{n} = 0$, and
(b) For each $i$ with $1\leq i\leq n$, either $x_{i} - x_{i - 1} = p$ or $x_{i} - x_{i - 1} = - q$.
Show that there exist indices $i < j$ with $(i,j)\neq (0,n)$, such that $x_{i} = x_{j}$.