Let
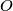
be the circumcenter and
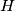
the orthocenter of an acute-angled triangle

such that
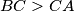
. Let

be the foot of the altitude
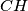
of triangle

. The perpendicular to the line
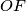
at the point

intersects the line

at

. Prove that
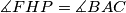
.
%V0
Let $O$ be the circumcenter and $H$ the orthocenter of an acute-angled triangle $ABC$ such that $BC>CA$. Let $F$ be the foot of the altitude $CH$ of triangle $ABC$. The perpendicular to the line $OF$ at the point $F$ intersects the line $AC$ at $P$. Prove that $\measuredangle FHP=\measuredangle BAC$.