Let

be a convex quadrilateral, and let
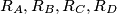
denote the circumradii of the triangles
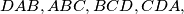
respectively. Prove that
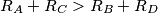
if and only if
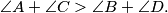
%V0
Let $ABCD$ be a convex quadrilateral, and let $R_A, R_B, R_C, R_D$ denote the circumradii of the triangles $DAB, ABC, BCD, CDA,$ respectively. Prove that $R_A + R_C > R_B + R_D$ if and only if $\angle A + \angle C > \angle B + \angle D.$