A finite sequence of integers
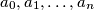
is called quadratic if for each

in the set
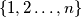
we have the equality
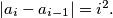
a.) Prove that any two integers

and
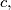
there exists a natural number

and a quadratic sequence with
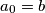
and
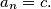
b.) Find the smallest natural number

for which there exists a quadratic sequence with
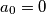
and
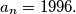
%V0
A finite sequence of integers $a_0, a_1, \ldots, a_n$ is called quadratic if for each $i$ in the set $\{1,2 \ldots, n\}$ we have the equality $|a_i - a_{i-1}| = i^2.$
a.) Prove that any two integers $b$ and $c,$ there exists a natural number $n$ and a quadratic sequence with $a_0 = b$ and $a_n = c.$
b.) Find the smallest natural number $n$ for which there exists a quadratic sequence with $a_0 = 0$ and $a_n = 1996.$