Let
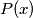
be a polynomial with real coefficients such that
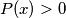
for all
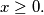
Prove that there exists a positive integer n such that
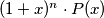
is a polynomial with nonnegative coefficients.
%V0
Let $P(x)$ be a polynomial with real coefficients such that $P(x) > 0$ for all $x \geq 0.$ Prove that there exists a positive integer n such that $(1 + x)^n \cdot P(x)$ is a polynomial with nonnegative coefficients.