Let
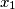
,
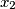
,

,
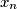
be real numbers satisfying the conditions:
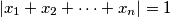
and
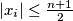
, for
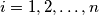
Show that there exists a permutation
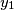
,
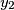
,

,
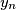
of
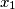
,
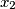
,

,
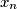
such that
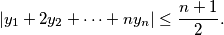
%V0
Let $x_1$, $x_2$, $\ldots$, $x_n$ be real numbers satisfying the conditions:
$ |x_1 + x_2 + \dots + x_n| = 1 $ and $|x_i| \leq \frac{n+1}{2}$, for $i = 1, 2, \dots, n$
Show that there exists a permutation $y_1$, $y_2$, $\ldots$, $y_n$ of $x_1$, $x_2$, $\ldots$, $x_n$ such that
$$| y_1 + 2 y_2 + \cdots + n y_n | \leq \frac {n + 1}{2}.$$