For every integer

determine the minimum value that the sum
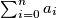
can take for nonnegative numbers
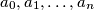
satisfying the condition
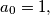
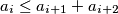
for
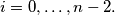
%V0
For every integer $n \geq 2$ determine the minimum value that the sum $\sum^n_{i=0} a_i$ can take for nonnegative numbers $a_0, a_1, \ldots, a_n$ satisfying the condition $a_0 = 1,$ $a_i \leq a_{i+1} + a_{i+2}$ for $i = 0, \ldots, n - 2.$