Ten points are marked in the plane so that no three of them lie on a line. Each pair of points is connected with a segment. Each of these segments is painted with one of  colors, in such a way that for any
colors, in such a way that for any  of the ten points, there are
of the ten points, there are  segments each joining two of them and no two being painted with the same color. Determine all integers
segments each joining two of them and no two being painted with the same color. Determine all integers  ,
, 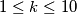 , for which this is possible.
, for which this is possible.
 colors, in such a way that for any
colors, in such a way that for any  of the ten points, there are
of the ten points, there are  segments each joining two of them and no two being painted with the same color. Determine all integers
segments each joining two of them and no two being painted with the same color. Determine all integers  ,
, 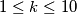 , for which this is possible.
, for which this is possible.  Školjka
Školjka