Školjka

%V0 There is given a convex quadrilateral $ABCD$. Prove that there exists a point $P$ inside the quadrilateral such that $$\angle PAB + \angle PDC = \angle PBC + \angle PAD = \angle PCD + \angle PBA = \angle PDA + \angle PCB = 90^{\circ}$$ if and only if the diagonals $AC$ and $BD$ are perpendicular. Proposed by Dukan Dukic, Serbia

%V0 Let $A_1A_2A_3...A_n$ be a regular n-gon. Let $B_1$ and $B_n$ be the midpoints of its sides $A_1A_2$ and $A_{n-1}A_n$. Also, for every $i\in\left\{2;\;3;\;4;\;...;\;n-1\right\}$, let $S$ be the point of intersection of the lines $A_1A_{i+1}$ and $A_nA_i$, and let $B_i$ be the point of intersection of the angle bisector bisector of the angle $\measuredangle A_iSA_{i+1}$ with the segment $A_iA_{i+1}$. Prove that: $\sum_{i=1}^{n-1} \measuredangle A_1B_iA_n=180^{\circ}$.

%V0 Let $ABCD$ be a convex quadrilateral. The perpendicular bisectors of its sides $AB$ and $CD$ meet at $Y$. Denote by $X$ a point inside the quadrilateral $ABCD$ such that $\measuredangle ADX = \measuredangle BCX < 90^{\circ}$ and $\measuredangle DAX = \measuredangle CBX < 90^{\circ}$. Show that $\measuredangle AYB = 2\cdot\measuredangle ADX$.

%V0 Let $ABC$ be a triangle such that $\angle ACB=2\angle ABC$. Let $D$ be the point on the side $BC$ such that $CD=2BD$. The segment $AD$ is extended to $E$ so that $AD=DE$. Prove that $$\angle ECB+180^{\circ }=2\angle EBC.$$ commentEdited by Orl.

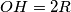
%V0 Let $ABC$ be a triangle, $H$ its orthocenter, $O$ its circumcenter, and $R$ its circumradius. Let $D$ be the reflection of the point $A$ across the line $BC$, let $E$ be the reflection of the point $B$ across the line $CA$, and let $F$ be the reflection of the point $C$ across the line $AB$. Prove that the points $D$, $E$ and $F$ are collinear if and only if $OH=2R$.

%V0 Let the sides of two rectangles be $\{a,b\}$ and $\{c,d\},$ respectively, with $a < c \leq d < b$ and $ab < cd.$ Prove that the first rectangle can be placed within the second one if and only if $$\left(b^2 - a^2\right)^2 \leq \left(bc - ad \right)^2 + \left(bd - ac \right)^2.$$