Let
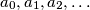
be an increasing sequence of nonnegative integers such that every nonnegative integer can be expressed uniquely in the form
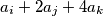
, where
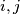
and

are not necessarily distinct. Determine
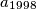
.
%V0
Let $a_{0},a_{1},a_{2},\ldots$ be an increasing sequence of nonnegative integers such that every nonnegative integer can be expressed uniquely in the form $a_{i}+2a_{j}+4a_{k}$, where $i,j$ and $k$ are not necessarily distinct. Determine $a_{1998}$.