The numbers from 1 to 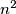 are randomly arranged in the cells of a
are randomly arranged in the cells of a 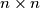 square (
square (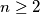 ). For any pair of numbers situated on the same row or on the same column the ratio of the greater number to the smaller number is calculated. Let us call the characteristic of the arrangement the smallest of these
). For any pair of numbers situated on the same row or on the same column the ratio of the greater number to the smaller number is calculated. Let us call the characteristic of the arrangement the smallest of these 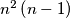 fractions. What is the highest possible value of the characteristic ?
fractions. What is the highest possible value of the characteristic ?
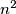 are randomly arranged in the cells of a
are randomly arranged in the cells of a 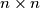 square (
square (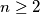 ). For any pair of numbers situated on the same row or on the same column the ratio of the greater number to the smaller number is calculated. Let us call the characteristic of the arrangement the smallest of these
). For any pair of numbers situated on the same row or on the same column the ratio of the greater number to the smaller number is calculated. Let us call the characteristic of the arrangement the smallest of these 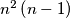 fractions. What is the highest possible value of the characteristic ?
fractions. What is the highest possible value of the characteristic ?  Školjka
Školjka