Let 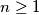 be an integer. A path from
be an integer. A path from 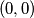 to
to 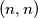 in the
in the 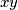 plane is a chain of consecutive unit moves either to the right (move denoted by
plane is a chain of consecutive unit moves either to the right (move denoted by  ) or upwards (move denoted by
) or upwards (move denoted by  ), all the moves being made inside the half-plane
), all the moves being made inside the half-plane 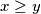 . A step in a path is the occurence of two consecutive moves of the form
. A step in a path is the occurence of two consecutive moves of the form 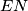 . Show that the number of paths from
. Show that the number of paths from 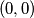 to
to 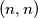 that contain exactly
that contain exactly  steps
steps 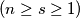 is
is
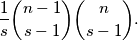
 be an integer. A path from
be an integer. A path from 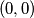 to
to 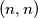 in the
in the 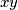 plane is a chain of consecutive unit moves either to the right (move denoted by
plane is a chain of consecutive unit moves either to the right (move denoted by  ) or upwards (move denoted by
) or upwards (move denoted by  ), all the moves being made inside the half-plane
), all the moves being made inside the half-plane 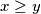 . A step in a path is the occurence of two consecutive moves of the form
. A step in a path is the occurence of two consecutive moves of the form 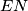 . Show that the number of paths from
. Show that the number of paths from 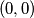 to
to 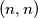 that contain exactly
that contain exactly  steps
steps 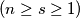 is
is 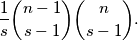
 Školjka
Školjka