Let

be a set of

residues
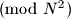
. Prove that there exists a set

of

residues
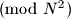
such that
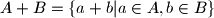
contains at least half of all the residues
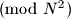
.
%V0
Let $A$ be a set of $N$ residues $\pmod{N^{2}}$. Prove that there exists a set $B$ of $N$ residues $\pmod{N^{2}}$ such that $A + B = \{a+b|a \in A, b \in B\}$ contains at least half of all the residues $\pmod{N^{2}}$.