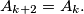Slični zadaci
A biologist watches a chameleon. The chameleon catches flies and rests after each catch. The biologist notices that:
- the first fly is caught after a resting period of one minute;
- the resting period before catching the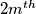 fly is the same as the resting period before catching the
fly is the same as the resting period before catching the 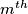 fly and one minute shorter than the resting period before catching the
fly and one minute shorter than the resting period before catching the 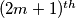 fly;
fly;
- when the chameleon stops resting, he
catches a fly instantly.
- How many flies were caught by the chameleon before his first resting period of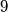 minutes in a row ?
minutes in a row ?
- After how many minutes will the chameleon catch his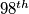 fly ?
fly ?
- How many flies were caught by the chameleon after 1999 minutes have passed ?
- the first fly is caught after a resting period of one minute;
- the resting period before catching the
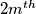 fly is the same as the resting period before catching the
fly is the same as the resting period before catching the 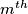 fly and one minute shorter than the resting period before catching the
fly and one minute shorter than the resting period before catching the 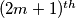 fly;
fly; - when the chameleon stops resting, he
catches a fly instantly.
- How many flies were caught by the chameleon before his first resting period of
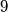 minutes in a row ?
minutes in a row ? - After how many minutes will the chameleon catch his
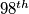 fly ?
fly ? - How many flies were caught by the chameleon after 1999 minutes have passed ?
Let 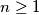 be an integer. A path from
be an integer. A path from 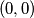 to
to 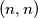 in the
in the 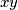 plane is a chain of consecutive unit moves either to the right (move denoted by
plane is a chain of consecutive unit moves either to the right (move denoted by  ) or upwards (move denoted by
) or upwards (move denoted by  ), all the moves being made inside the half-plane
), all the moves being made inside the half-plane 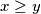 . A step in a path is the occurence of two consecutive moves of the form
. A step in a path is the occurence of two consecutive moves of the form 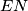 . Show that the number of paths from
. Show that the number of paths from 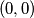 to
to 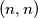 that contain exactly
that contain exactly  steps
steps 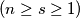 is
is
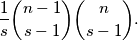
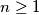 be an integer. A path from
be an integer. A path from 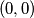 to
to 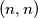 in the
in the 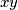 plane is a chain of consecutive unit moves either to the right (move denoted by
plane is a chain of consecutive unit moves either to the right (move denoted by  ) or upwards (move denoted by
) or upwards (move denoted by  ), all the moves being made inside the half-plane
), all the moves being made inside the half-plane 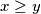 . A step in a path is the occurence of two consecutive moves of the form
. A step in a path is the occurence of two consecutive moves of the form 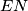 . Show that the number of paths from
. Show that the number of paths from 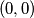 to
to 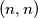 that contain exactly
that contain exactly  steps
steps 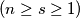 is
is 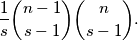
Show that for any finite set  of distinct positive integers, we can find a set
of distinct positive integers, we can find a set  ⊇
⊇  such that every member of
such that every member of  divides the sum of all the members of
divides the sum of all the members of  .
.
Original Statement:
A finite set of (distinct) positive integers is called a DS-set if each of the integers divides the sum of them all. Prove that every finite set of positive integers is a subset of some DS-set.
 of distinct positive integers, we can find a set
of distinct positive integers, we can find a set  ⊇
⊇  such that every member of
such that every member of  divides the sum of all the members of
divides the sum of all the members of  .
. Original Statement:
A finite set of (distinct) positive integers is called a DS-set if each of the integers divides the sum of them all. Prove that every finite set of positive integers is a subset of some DS-set.
 Školjka
Školjka  be a set of
be a set of 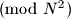 . Prove that there exists a set
. Prove that there exists a set  of
of 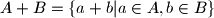 contains at least half of all the residues
contains at least half of all the residues  and
and  be odd integers so that
be odd integers so that 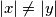 . Show that there are two integers of the same colour whose difference has one of the following values:
. Show that there are two integers of the same colour whose difference has one of the following values: 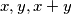 or
or  .
. 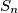 be the number of sequences
be the number of sequences 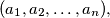 where
where 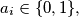 in which no six consecutive blocks are equal. Prove that
in which no six consecutive blocks are equal. Prove that 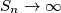 when
when 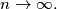
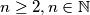 and
and 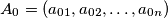 be any
be any 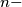 tuple of natural numbers, such that
tuple of natural numbers, such that 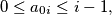 for
for 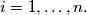
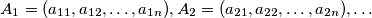 are defined by:
are defined by: 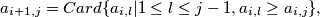 for
for 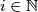 and
and 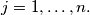 Prove that there exists
Prove that there exists 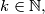 such that
such that