Let

be an even positive integer. We say that two different cells of a
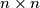
board are neighboring if they have a common side. Find the minimal number of cells on he
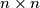
board that must be marked so that any cell marked or not marked) has a marked neighboring cell.
%V0
Let $b$ be an even positive integer. We say that two different cells of a $n \times n$ board are neighboring if they have a common side. Find the minimal number of cells on he $n \times n$ board that must be marked so that any cell marked or not marked) has a marked neighboring cell.