Suppose that every integer has been given one of the colours red, blue, green or yellow. Let

and
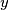
be odd integers so that
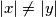
. Show that there are two integers of the same colour whose difference has one of the following values:
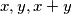
or

.
%V0
Suppose that every integer has been given one of the colours red, blue, green or yellow. Let $x$ and $y$ be odd integers so that $|x| \neq |y|$. Show that there are two integers of the same colour whose difference has one of the following values: $x,y,x+y$ or $x-y$.