Let
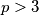
be a prime number. For each nonempty subset

of
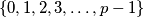
, let
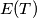
be the set of all
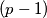
-tuples
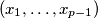
, where each
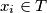
and
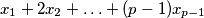
is divisible by

and let
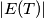
denote the number of elements in
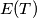
. Prove that
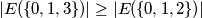
with equality if and only if
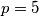
.
%V0
Let $p >3$ be a prime number. For each nonempty subset $T$ of $\{0,1,2,3, \ldots , p-1\}$, let $E(T)$ be the set of all $(p-1)$-tuples $(x_1, \ldots ,x_{p-1} )$, where each $x_i \in T$ and $x_1+2x_2+ \ldots + (p-1)x_{p-1}$ is divisible by $p$ and let $|E(T)|$ denote the number of elements in $E(T)$. Prove that
$$|E(\{0,1,3\})| \geq |E(\{0,1,2\})|$$
with equality if and only if $p = 5$.