Prove that there exists two strictly increasing sequences
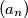
and
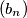
such that
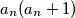
divides
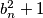
for every natural n.
%V0
Prove that there exists two strictly increasing sequences $(a_{n})$ and $(b_{n})$ such that $a_{n}(a_{n}+1)$ divides $b^{2}_{n}+1$ for every natural n.