Let
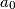
,

,
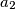
,

be a sequence of positive integers such that the greatest common divisor of any two consecutive terms is greater than the preceding term; in symbols,
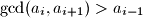
. Prove that
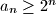
for all
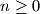
.
Proposed by Morteza Saghafian, Iran
%V0
Let $a_0$, $a_1$, $a_2$, $\ldots$ be a sequence of positive integers such that the greatest common divisor of any two consecutive terms is greater than the preceding term; in symbols, $\gcd (a_i, a_{i + 1}) > a_{i - 1}$. Prove that $a_n\ge 2^n$ for all $n\ge 0$.
Proposed by Morteza Saghafian, Iran