Let  be a positive integer and
be a positive integer and 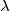 a positive real number. Initially there are
a positive real number. Initially there are  fleas on a horizontal line, not all at the same point. We define a move as choosing two fleas at some points
fleas on a horizontal line, not all at the same point. We define a move as choosing two fleas at some points  and
and  , with
, with  to the left of
to the left of  , and letting the flea from
, and letting the flea from  jump over the flea from
jump over the flea from  to the point
to the point  so that
so that 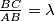 .
.
Determine all values of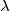 such that, for any point
such that, for any point  on the line and for any initial position of the
on the line and for any initial position of the  fleas, there exists a sequence of moves that will take them all to the position right of
fleas, there exists a sequence of moves that will take them all to the position right of  .
.
 be a positive integer and
be a positive integer and 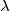 a positive real number. Initially there are
a positive real number. Initially there are  fleas on a horizontal line, not all at the same point. We define a move as choosing two fleas at some points
fleas on a horizontal line, not all at the same point. We define a move as choosing two fleas at some points  and
and  , with
, with  to the left of
to the left of  , and letting the flea from
, and letting the flea from  jump over the flea from
jump over the flea from  to the point
to the point  so that
so that 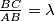 .
. Determine all values of
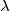 such that, for any point
such that, for any point  on the line and for any initial position of the
on the line and for any initial position of the  fleas, there exists a sequence of moves that will take them all to the position right of
fleas, there exists a sequence of moves that will take them all to the position right of  .
.  Školjka
Školjka