A number of  rectangles are drawn in the plane. Each rectangle has parallel sides and the sides of distinct rectangles lie on distinct lines. The rectangles divide the plane into a number of regions. For each region
rectangles are drawn in the plane. Each rectangle has parallel sides and the sides of distinct rectangles lie on distinct lines. The rectangles divide the plane into a number of regions. For each region  let
let 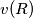 be the number of vertices. Take the sum
be the number of vertices. Take the sum 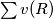 over the regions which have one or more vertices of the rectangles in their boundary. Show that this sum is less than
over the regions which have one or more vertices of the rectangles in their boundary. Show that this sum is less than 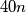 .
.
 rectangles are drawn in the plane. Each rectangle has parallel sides and the sides of distinct rectangles lie on distinct lines. The rectangles divide the plane into a number of regions. For each region
rectangles are drawn in the plane. Each rectangle has parallel sides and the sides of distinct rectangles lie on distinct lines. The rectangles divide the plane into a number of regions. For each region  let
let 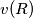 be the number of vertices. Take the sum
be the number of vertices. Take the sum 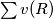 over the regions which have one or more vertices of the rectangles in their boundary. Show that this sum is less than
over the regions which have one or more vertices of the rectangles in their boundary. Show that this sum is less than 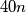 .
.  Školjka
Školjka