Let

and

be relatively prime positive integers. A subset

of
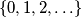
is called ideal if
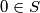
and for each element
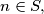
the integers
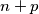
and
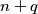
belong to
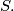
Determine the number of ideal subsets of
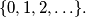
%V0
Let $p$ and $q$ be relatively prime positive integers. A subset $S$ of $\{0, 1, 2, \ldots \}$ is called ideal if $0 \in S$ and for each element $n \in S,$ the integers $n + p$ and $n + q$ belong to $S.$ Determine the number of ideal subsets of $\{0, 1, 2, \ldots \}.$