Let
be the circumcenter and
the orthocenter of an acute triangle
Show that there exist points
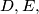
and
on sides
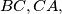
and
respectively such that
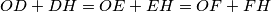
and the lines
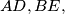
and
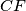
are concurrent.
%V0
Let $O$ be the circumcenter and $H$ the orthocenter of an acute triangle $ABC.$ Show that there exist points $D, E,$ and $F$ on sides $BC,CA,$ and $AB$ respectively such that $$OD + DH = OE +EH = OF +FH$$ and the lines $AD, BE,$ and $CF$ are concurrent.
Školjka