Let
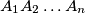
be a convex polygon,
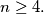
Prove that
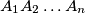
is cyclic if and only if to each vertex
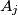
one can assign a pair
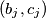
of real numbers,
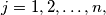
so that
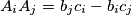
for all
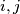
with
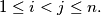
%V0
Let $A_1A_2 \ldots A_n$ be a convex polygon, $n \geq 4.$ Prove that $A_1A_2 \ldots A_n$ is cyclic if and only if to each vertex $A_j$ one can assign a pair $(b_j, c_j)$ of real numbers, $j = 1, 2, \ldots, n,$ so that $A_iA_j = b_jc_i - b_ic_j$ for all $i, j$ with $1 \leq i < j \leq n.$